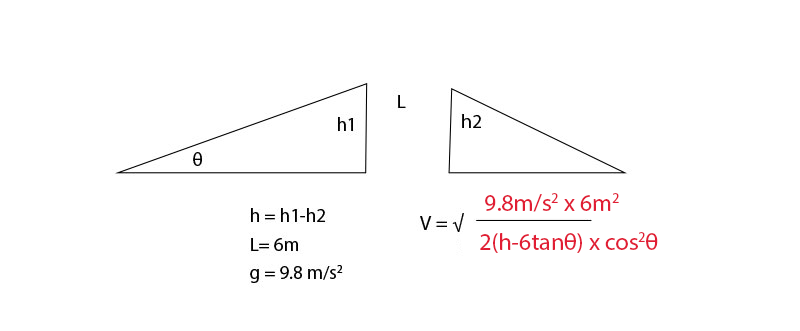
If h is the difference in height between the two sides of the gap, θ is the angle of the exit’s slope, V is the velocity, and g is the standard acceleration of free fall at 9.8 m/s2, the required velocity would equal to square root of 9.8m/s2 *6m2 divided by 2(h-6tanθ)*cos2θ…
We have now gotten so much conflicting feedback on this equation, that we have come to beg for a crowd consensus. Please excuse poor Illustrator skills.
A car is travelling up a slope and is about to jump a gap.
Yes, no?
Update: everything is funnies to you, isn’t it?

I’m not helping with maths, just laughing and laughing. IT WILL MAKE IT! I am from the Top Gun school of physics, where you just have a need, a need for SPEED. And all is well.
You and Alessandro agree.
I kept my voice calm. “Alessandro, you’re going to kill us. This only works in the movies and it requires a ramp. The moment our wheels leave the ground, the car will start dropping. Even if we make it, the car will crumple from the impact.”
“It will be fine.” The Alfa roared up the slope, accelerating.
“How? How will it be fine?”
He looked over at me. “This car is very light and we’re going to drive very fast.”
If the Dukes can do it, so can they (and the Dukes weren’t exactly using a lot of brainpower).
But the Dukes had the General Lee!
+1 and *snorts*
My math skills may be horrible, but who cares. I need an Alessandro in my life! 😀
Why don’t you just visit the nearest high school, tackle a physics teacher and then distract him with the math?
My high school physics teacher was as old as the hills, and the chemistry teacher was even older. No way would ever tackle either of them! Now, there were some phys ed teachers it might have been worth tackling… Naw, I was a 98-pound weakling in high school. I couldn’t even get the chemistry teacher down!
Love this! I agree with Alessandro as well! Although physics and science are all “factual” and such, these are works of fiction and who doesn’t like breaking some laws?
It always worked for the Duke Boys
But they aren’t driving General Lee!!!!
Oh my gosh. Hire someone. That just looks like too much brain power. It makes my brain hurt.
Good luck. Peace light and love ?K
Regardless of the math, I think the final answer would be splat…you could ask Arabella!
LOL. +1
Give the car a bigger engine. /nod. That is always the answer. Possibly wings.
+1
Bigger engines weigh more..?
That’s okay. The bigger engine can weigh more as long as it provides sufficient acceleration and zoom zooms. The zoom zooms are very important. (And realistically, the bigger engine will give so much zoom zooms it’s all good.)
Zoom zooms = go go = wheee flight!
This math is so much better than that other math other people are discussing.
Zoom zooms = good. Go go, little characters in the zoom zooms!
Why, uh, yes… I had some sugar today? Why are you looking at me like that…
Bwahahahaha!
See also, Jet engines are big f*ckers and give lots of zoom-zooms.
A rocket. And get that vector right…!
(This should totally be my sort of problem, and maybe it will a bit later. But a) the weather is messing with me. And b) a few of my physics simulations are having conniptions, maybe because of some backwards compatibility issues with my code, so I’ve been debugging not that well documented python wrappers for most of the day.)
(Ngaaahhh! Stupid titanium plate! Weather should be fun, it shouldn’t hurt!)
I saw rocket and pictured Wile E. Coyote behind the wheel. Have Catalina point out to Alessandro how well this situation didn’t work for poor Wiley.
??
If it is not addition, multiplication, subtraction or division
Who cares
Car wings works for me?
+1 for wings
Sending moral support. Aside from the fact that I just relented and took my good pain meds, I can’t even begin to help. In fact it looks like it might hurt a brain. Good luck!!
Erm sorry I did physics over 20 years ago and my brain is mush from children! But looks right to me
Or you could get an air mage to pop up at the right moment to give them a lift? Then you don’t have to worry about physics?
+1
Air mage or big eagles. Ask Gandalf.
At some point you’re going to have to make a conversation to miles per hour for those of us in the states. Right now the formula uses meters. I remember gravity acceleration being 32 feet per second squared.
heh, I’m the opposite – thou I can’t be of any help since my math has become rusty after high school – but it’s soooooo nice to see something in meters instead of miles/feet/etc!
I’m from Latvia, Europe and whenever I read books, watch movies etc quite often they have people’s height or other stuff in feet, inches and so forth or weight in pounds or whatever other variety of measure that are not meters or kilograms and not to mention weather in fahrenheit…I’m like – whyyyyy? I don’t get it! and don’t want to look it up in google to convert to measurement I understand aka m/kg/°C
hehhehehe , never thought I’d be so happy to just look at formulas with meters XD
Even if I can’t solve it, at least I understand it ;D
Go see the car jump scene by CE Murphy. Combines magic and her special muscle car for a truly magical scene. It is her Walker series.
I was thinking of that one too!
This is why my degree was in History!
+1
Let me run this past the math teacher down the hall and get back to you. (I teach technology, and my math expertise ends at algebra.)
Yes, a sensible person. This looks just like an exam question. Teachers to the rescue!
Okay, here’s what he said, after throwing a bunch of math gibberish (cleverly disguised as English words) at me:
“Keep in mind: the tilt or angle of the car will not change appreciably while it’s in the air, and this has to be taken into account for the angle of the second ramp. If it’s tilted down (or indeed at any angle less than the angle of the car), the rear tires will hit before the front, which will slam the front of the car down. If the car hits too far down the ramp, the rear bumper might hit before the tires which would REALLY slam the front end down and probably do body damage.
Unless the car is going so slowly that the back tires are on the ground long enough for the front end to start falling appreciably before the back end leaves the ramp. And that’s a whole ‘nother calculation!”
So, in a short answer: No, it won’t work.
And if you wanted to know the math gibberish, let me show you it:
“The vector of the car’s velocity heading up the ramp needs to be broken into a vertical component and a horizontal component. The horizontal component will be how fast the car crosses the gap. The vertical component will be what is working against gravity. Let’s say the car is going V0 when it hits the end of the ramp (for ease of computations we will take the car to be a point – the bottom of the rear tires). This is the hypotenuse of the right triangle we use to break the velocity into its two components. We will find the horizontal and vertical components using SOHCAHTOA.
“The vertical component VV will be V0sinθ. Note that the velocities have to be given in meters per second. The horizontal component Vh will be V0cosθ. So the car’s height above the ground (in meters) for any second s after it leaves the end of the ramp will be h(s)= –9.8s2 + V0(sinθ)s + h1.(parens for clarity)
“Using this you can determine when the car will hit the opposite ramp at height h2 by setting the equation equal to h2. Then solve for s using the quadratic formula.
“Once you know how many seconds the car will be in the air, you can determine how far it will have traveled. Call that distance d. d= V0(cosθ)s. That’s the maximum distance the second ramp can be from the first.”
So. Yeah.
You forget that momentum plays into this. For example you hit the brakes in the air the car will nose dive in the air. You keep on the gas and you will tend to keep the front end up. Also since the front end is heavy it typically comes down first. Youtube has many examples. More applicable to lighter vehicles but it does still work to a degree. i.e. dirt bikes hitting jumps. You correct your position by gas or brake as needed.
Right, but you can’t brake in mid-air. Once you leave the ground, the only things that can slow you down or change your direction are gravity, drag, or impact with another object. For a short jump, you’re basically going the speed you’re going, in the direction you were going, in roughly the same the position you were in when you left the ground (because cars are rigid), until you hit the ground again. If you stay in the air long enough, the front end will begin to tilt down enough to hit before the back end, but it depends on the length of the jump. You’d need a certain amount of hang time in order for that to occur.
Actually you can. You are forgetting the effect of torque. If you brake, you will slow down the rotation of the tires, which will increase the rotation of the car body and vice versa.
Maybe they could throw their weight forward while in the air to help bring the front end of the car down…
The Mythbusters were bound to try this sometime try you tube.?zoom zoom?
Before getting involved in the math….
The gap (L) is only 6 meters????
Come on. They don’t even need to accelerate.
I know, I know. It’s the integrity of the math. And once upon a time I may have even known the math. But 6 meters? You could use E=mc squared and they’d make it. Plus, you know, beginning of the story. How could they not?
Weeell, technically they can nose dive there if the speed is low enough, and this is technically and overpass so the ramp angle is low, but if we mess up the equation, we will get 50 emails about it.
But it’s a light car and they’re going to drive very fast!
?
I know, I know. Not very helpful.
Actually, the weight of the car is not part of the equation… a heavy car will be slowed down less by air drag – unless it is an SUV with worse aerodynamics…
You’d only get 50 emails if you get it wrong? Wow, I would think it would be in the hundreds.
MAGIC DOESN’T HAVE TO FOLLOW THOSE PESTY REAL WORLD LAWS.
6 meters is approx. 20ft,or two stories of a building. That seems quite a bit to cross? Is it really so little?
?????
Mythbusters has done this with the rocket car / jet car. it spectacularly exploded, and it’s one of my favorite episodes. It was one of their early, early episodes! Of course, they attached JATO rockets to the car which is not realllly the case here, but they totally did launch the vehicle up a ramp.
Totally worth the watch for fun.
Also, I never thought this would EVER be relevant anywhere, but here is the UK car jumping championship:
https://www.youtube.com/watch?v=3HUqWb6hyTU
https://mythresults.com/unarmed-and-unharmed
Does MythBusters help with the Speed bus jump?
A bus can jump over a 50-foot gap in a roadway, land safely on the other side, and continue driving.
BUSTED
The Build Team acquired a bus with the same dimensions as that used in the film, then built a small-scale model of it as well as the stretch of road in question. Running at a calculated speed of 20 miles per hour, the bus plunged off the end of the road and crashed into the support posts at ground level on the other side. When the gap was halved, the bus still dropped far enough to hit the far end of the roadbed head-on. The team theorized that hidden ramps placed on either end of the gap may have helped the bus to make its jump safely. After outfitting their full-size bus for remote-control steering on an airfield, they did a speed test and found that it could go up to 58 miles per hour, rather than the 70 miles per hour depicted in the film. With the 50-foot target distance scaled down to allow for the lower top speed, they jumped the bus off a ramp; it fell far short of the target, but remained relatively intact until it hit a concrete safety barricade. Since the bus could not make the jump, the team declared the myth busted.
Kelly, I can google. I really can. I’m asking for help to proofread the formula. Your example is not helpful because math. 🙂
Sorry, I think I misunderstood the question. I didn’t realize the formula was going into the book. Definitely no help there.
I am teasing you. 🙂 Most other people just made fun of the whole thing, heh.
Urban myth. Tower Bridge in London, England is a bascule bridge (it opens to allow shipping to pass underneath). Legend has it that. A double decker red London bus was already starting to cross as bridge opened, and the driver put his foot down and the bus leapt the gap …
If he had, the (wooden) roadbed of the bridge would have collapsed under the weight of the crashing bus!
It helps if it’s dark and you’re wearing sunglasses…
(English major, x may remain unknown.)
+1 for Blues Brothers reference.
The base problem is a textbook ballistics calculation. Then you solve for V instead and ignore niggling details like car centers of mass, air resistance, and whatever else.
If someone doesn’t verify your work sooner, I’ll crack open the old physics textbook after my kids go to bed and see what I can do ?
Do it. I’m getting sort of curious about the math.
Same +1
It’s projectile movement and I am 98% sure it’s right. But it doesn’t hurt to check…
I wish you the bestest luck.
There is a reason why I am a librarian. Sadly I am no help.
If it makes you feel better, I am always comforted by your technical explanations of things. I don’t really understand them but it comforts me to know that you do.
I realize some people are picky and will natter at you if they don’t think it’s correct.
So again, good luck!
I would rather be taking my chances as a crash text dummy in the car than diving into that equation! But I definitely respect and applaud all your efforts to write a plausible story. Can’t wait to get my hands on it!
It is correct as long as you are squaring the 6 in the numerator. (Assuming that the length of the gap is 6 meters and the car is not accelerating except for gravity).
So required velocity is the square root of 9.8m/s2 *6^2m2 divided by 2(h-6tanθ)*cos^2θ
You are so awesome. Thank you!
Hmmm… so as long as the angle is reasonable (between 35 and 43 degrees) it’s doable. I need to get to my calculator.
What’s the h?
Sorry, the – is wrong. Make L large enough and you get an imaginary velocity…
Are you certain of that? Because I’m getting that the minus sign in the denominator should be a + sign.
Where that comes from… The vertical motion is y(t)=y0+v0*t-0.5*g*t^2. The initial height is 0, and the final height should be -h. I’m treating the upward direction as positive, so the initial velocity v0 is v*sin(theta). This means the equation I’m solving is:
-h = v*sin(theta)*t-0.5*g*t^2
The sin(theta) term is what eventually yields the tan(theta) in the denominator. So it needs to have the same sign as h in the final answer.
Sanity check: Suppose the car is pointing almost vertical, so theta is almost 90 degrees and tan(theta) is very large (approaching infinity). The formula above with the minus sign would say that h-L*tan(theta) is negative, so it’s impossible to find an initial velocity that works. (In fact, since L is probably bigger than h, it’ll say there’s no answer even if the angle is 45 degrees.) If you switch the minus to a plus, the quantity under the root is no longer negative, and an answer exists.
Credentials: PhD in physics, but I teach math so I don’t solve these problems on a regular basis.
I agree.
I agree. The correct answer: v = sqrt(gL^2/(2*(h+L tan(theta))*cos^2(theta)))
Plus in the denominator not negative. Acceleration of gravity should be negative.
Credentials: PhD in aerospace engineering
…can I sit at this table?
+1 ?
Win.
Our calculation matches your assertion that it should be a plus sign in the denominator.
I wish I could give this response a thumbs up. I haven’t had to do math like this since I was in high school and that was 10 years ago now. Needless to say I’m not a help here but it’s fun watching someone else explain it and look at the math. That why I watch minute physics and other YouTube channels like it.
Yup, good point. Darn sign conventions.
I just asked a friend of mine who is a physics nerd, lets see if he responds
There isn’t enough information to solve the problem. If you simplify the problem by closing the gap between the two ramps, you see the difficulty – The vehicle has a length that is not zero and the weight of the vehicle is not evenly distributed front to rear. Simplify a bit more, spread the weight so it is evenly distributed front to rear. The problem is really one of having the vehicle completely clear the on ramp (right side, I think) while in the air so that it lands on the off ramp and doesn’t get hung up. Now move the ramps apart and repeat. The answer (still simplified) is to extend the on ramp with an imaginary line that continues across the gap and a further distance of the length of the vehicle. This will ensure that there is no hang up but it exceeds the minimum requirement. Now just solve for the uneven distribution of the weight the the fact that we don’t know the length of the vehicle and it’s a done deal. I really suggest that you just use magic. 🙂
You are thinking too complicated… just add 10% to the result and you can neglect air resistance and car length…
This is also correct, but if we assume the car is a point mass and only think about the kinematics, the equation is correct.
And give thanks that you’re dealing with rigid body dynamics!
…heh, this would be fairly easy to simulate. (Which I only mention because the end product would be a cute little movie.)
Checking with my math major kid. If not, will check with the husband. Grr…maths
Horizontal Velocity at exit = V cos(theta)
Vertical Velocity at exit = V sin(theta)
Disregard car rotation, car angle, and air resistance, you are solving for V, where the time to travel 6m horizontally is less than or equal to the time that the car would go up and down h (h2-h1)
so, t = 6/(V * sin(theta)). Displacement, vertically, is given by d = Vy * t + 1/2 * a * t^2. Substituting the known values,
-h = V * cos(theta) * 6 / (V * sin(theta)) + 1/2 * 9.8 *(6 / (V * sin(theta))^2
Solving for V, we have
V = sqrt ( (g * d^2)/ (2 * (- h – cot(theta) * d) * sin(theta)^2))
I think.
where 9 =9.8, d = 6, and h = h1-h2, and theta is the angle of the ramp.
And do not put a – in front of h – or the square root will ruin your day… 😉
Grr, got my sin and cos messed up. everyone else are more correct.
I would note that -h is correct, as it is h1 – h2. Since up in the y axis is positive, the distance in the y direction traveled needs to be -h, not h. (if h2 is 10m lower than h1, you want vertical displacement to be -10. But h1-h2 is 10 (positive).
V = sqrt ((g *d^2) / (2 * (-h – tan(theta) * d) * cos(theta)^2))
… and now you always get an imaginary velocity… 😉
no, because g is negative. the numerator is -9.8 * 6^2…
When solving for t, you used the vertical velocity when you should have used the horizontal velocity. So you need to switch all your sines and cosines.
Ok, bachelor in physics and master in computer science here.
According to my calculations, the formula has one mistake: it needs to be
2* ( h + L tan Theta) * cos 2 Theta
in the denominator under the square root. +, not – in the parenthesis.
BTW, how much is h? So we can calculate v…
Based on the derivation of this equation, it looks correct, but it has been years since I did this type of math myself. Hopefully an up-to-date physics person can verify.
My degree is in statistics, not physics but it looks accurate aside from any wind resistance, which you can argue is minimal, and not accounting for the effect of the impact on the car. I have no idea if the car would be able to drive afterwards but yes, the formula looks correct.
Too bad Rogan isn’t nearby? If he can make a bus fly……
I appreciate the fact checking you guys do when you write and look forward to the book. Thank you.
The Rogan factor needs to be accounted for
There’s a minor mistake:
Replace h – 6 tan(theta) with h + 6 tan(theta).
I just went through the math, and that’s what I concluded. To convince yourself, consider what happens if h2 = h1. That makes h = 0, and impossible to get a real velocity which satisfies the equation. But we know the jump is possible when h1 = h2.
Hope that helps!
I’m a senior in aerospace engineering and this took me…. an embarrassing amount of time to figure out. But if you’re looking for more confirmation, the equation you have matches what I got: V = sqrt(( gL^2)/((y-Ltan(theta))*(2*cos^2(theta)))), if y is the vertical distance you want to cross and L is the horizontal distance. I doubt you want to look at more equation derivations at this point but let me know if you want my scribbles.
Nope, you also have the wrong -.
Yeah, to be specific this answer is for h2 > h1! And I’m using -9.8 m/s^2 for g, instead of positive 9.8. But in my defense, no one should be expected to keep sign conventions straight while speeding towards a ramp/cliff.
Hope this helps: comments on my phone are not a good tool for formulas:
If you use simple parabolic flight (no air resistance) the formulas are as follows:
Dx= vx •t, where vx is the x component of your car speed, thus vx=v • cos theta
Dy = -0.5•g•t^2
You need to cross distance Dx = L so
Some math makes t = L/vx
Filling in t in the formula for the height
Dy=h2-h1=-h=-0.5•g•(l/vx)^2
Solving vx from that:
Vx= sqrt(0.5•9.8•6^2/H)=v•cos theta
So v= sqrt(176,4/h)/cos theta
Off course I ignored the upward speed of the car here, but that makes this so much easier 😉
Sorry I can’t help because I was an English major. I’m having trouble right now because my doctor changed my daily medication and instead of giving me a two week supply at a time I get it a month at a time. I can’t figure out if he has doubled my dosage, halved it, or left it the same. I actually had to sit down with pencil and paper to figure it out. Getting old has some wonderful benefits but improved memory is not one of them.
Reading these brilliant people responding, my head is spinning! I’m terrible at math, and so envy those of you who aren’t:)
I would have loved this problem when I was majoring in Engineering Physics! Theeeeeen I got bored of math and switched to something that didn’t make my brain hurt. Now I program computers and make THEM (and google) do this kind of stuff for me :p
My grade 12 (that is senior math for my American co-readers) math teacher passed me because in grade 12, I never missed a math class or an opportunity for help or tutoring…. and I still failed. Call MIT, this is way beyond my scope. Now, I am a published book reviewer and columnist, I do know how to edit so if you need that in non-fiction, I am all about it.
🙂
You can come up with all sorts of intermediate and indeterminate formulae, but if you don’t know the lateral distance between h1 and h2, you have nothing meaningful.
Online calculator to check your math: https://www.omnicalculator.com/physics/projectile-motion
And then the air bags go off ….
Hi,
Find the result below in a pic, if a detailed derivation is required I can make one, and send you the pdf.
cheers,
Marton
+1
Yes, Physics professor here, same result as Marton
Forgot my cerdentials: MSc in physics and working on phd, my research topic is general relativity
I’m a college math professor, but this is really more of a physics problem and not something that I’m called upon to do on a regular basis, so I would need to look up the formulas in question.
I e-mailed this to our physics teacher here at school because it should be right in his wheelhouse. Hopefully, I will have an answer in my In Box when I get back from my class.
What you have there is an equation for velocity only it is not going to tell you the required velocity to jump a vehicle over a gap between two incline planes that whould include the speed of the vehicle its wheight and and the angle off aproch. I’m not sure what the proper equation is but i dont think the one your using is appropriate.
6m^2 should be (6m)^2 or 36m^2, as someone already noted. g should be -9.8m/sec^2 (it’s negative, remember: gravity sucks). h is h2-h1 (it also should be negative: we’re going down). I don’t remember enough physics to verify the rest of the equation (I used to do math/statistics stuff, not ballistics).
You need a physics person to check the equation … and an engineer to fudge the result 🙂
You might want to consider graphing the launch parameters and using the graph to determine the gap and the destination height. The weight distribution of the car is pretty critical: if the car is heavier in the back, it will rotate the wrong way (backward) during free flight; and if it doesn’t tilt forward just right, the impact on landing will be messy.
How fast is the tailwind? 🙂 🙂
Love you both! Thanks for inviting us to “play”!
hi ilonna and gordon,
i think it maybe the equation is over complicated. From what i understand from the writing you are now going into trajectory formula. i think your dad might be able to do that in his sleep. all you have do is plug how fast the car is going and the distance you want to reach if you want to know the ideal angle you want. There are plenty of trajectory simulator out there you can use. i havent seen the one gericke pointed but younguys got this. you know most of the variables, and because your authors can just say what they are. Although I am curious which unit of measure you will go with. grams or pounds, feet or kilometers, etc. love your books!!
oh one other thing if the math is wrong alessandro had a secret passive XD
Part 1/3
Part 2
Part 3 and obviously this is ignoring a lot of variables and positive y is in the “up” direction
Your Delta y is wrong. It is + 1/2 g t^2, not –
I set the “up” direction as positive. Gravity is a downward force here so it’s negative and the velocity in the y is positive. I can put in made up test numbers if you want and show that a positive g will end in the square root of a negative number which will end with an imaginary number for the velocity.
It is still wrong, unless your Delta h is also negative…
The point is: the distance fallen due to gravity must be equal to the height difference of the ramps plus the height gained through the jump.
Authorlords,
Professor Stephen Hawking (one of the greatest mathematician/ physicists who ever lived) observed that he had been told that his readership for The Brief History of Time would HALVE for every equation he included …
Please say this is only for research, and not for inclusion!
Don’t worry, it is funny.
I, too, just sat here and read over the wonderful computations without even pretending to understand them. There are many people with great minds on this blog.
I am a Null with numbers. However, just if you ever need me: I am Significant with history but I am a Prime if you ever need any thoroughbred racing information, especially pedigrees.
It is correct. I googled mortar trajectory, which took me to the trajectory formula from physics. Rearrange the equation to solve for v. Of course, doesn’t include wind resistance which is a big number for a car traveling at speed.
Too bad Rogan can’t just float the car over 😀
Not a math person, makes my eyes cross. Amazing the variety of people/professions that tune in here. Always interesting.
Me, too. My math skills end at intersecting trains. Currently I am doing the following math: How many types of math professionals does it take to get a car across a theoretical gap in the road of an urban fantasy novel.
LOL and very strongly agree!!
Math? What you need to tell is the type of vehicle and the size of the engine in the vehicle. If you are driving an electric, eco friendly vehicle, find a bridge. If you are driving an American muscle car with a big V8 engine, topped by a 4 barrel Holly carburetor and have a full tank of gas, floor it and fly. Anything in between those two vehicles needs more consideration.
A similar piece of brain candy was used in playing with the bus jumping scene in the movie Speed.
https://maththrills.com/speed/
Just wow, I have no idea . I am with Alessandro, just drive very fast, and cross your fingers.
This math is too complicated for me.
But I am in awe of the many math/ physics professionals that have responded to the question.
I got a bunch of problems, but I don’t know how many, because math is one. Good luck! Maybe a little magical assist will help the Alfa make the leap.
OK, let’s just get our heads around this.
First step is to ballpark.
You say Alessandro is driving “very fast.” Suppose that is 100 mi/hr. (They’re in a suburban / urban zone, right? So let’s take that as an upper limit.) We need to convert this to meters/sec.
1 mile = 1609.34 m. Let’s call it 1600 m. 100 mi = 1600×100 = 160,000 m.
1 hr = 60 min = 3600 sec.
So 100 mi/hr = 160,000 m / 3600 sec = 1600/36 = 44.4444 (etc) m/s (meters / sec), and let’s call that 44 m/s. That’s like covering almost the length of a basketball court (50 feet in length) in one second. Pretty fast, but doable.
This distance along the ramp breaks down into two components; one going horizontal, and the other going vertical. They don’t add, precisely. Instead, they follow the “hypotenuse law.”
You have a picture of a triangle (ramp). d (distance along the ramp incline) squared = dh squared + du squared. (Meaning, the total distance-along-the-ramp squared equals your horizontal distance (going forward) squared plus your distance-up (going up) squared.)
The distance along the inclined ramp is the long side (the ramp side) of the triangle. Of the two components, the vertical distance (du, going up) is the opposite side of your angle (theta). This is “sin theta.” The distance going forward – the horizontal distance – is the adjacent (or bottom, horizontal) side of the triangle. This is cosine theta, or “cos theta.”
You’re calling your vertical distance (height up) on the first ramp h1. (That was my dh.)
You’re calling your vertical distance (height up) on the second ramp h2.
You’re calling the difference between the two heights = h = h1-h2.
You’re calling the separation between the two ramps L = 6 m.
I think it might be too precise to try to work an exact height for h and/or h1 & h2, because it might be more intuitively helpful to set up some scenarios and work through them.
If there is anything at all real-world about this scenario, the ramp incline should not be too extreme. Just did a Google search. 15% grade (tangent, or sin / cosine) is often the steepest grade that civil engineers want to build. Some of the steepest grades in San Francisco are 35%. That’s very steep.
Let’s just play with a ramp angle of 20 degrees. The cosine of 20 degrees is about 0.94.
The sin of 20 degrees is about 0.34. The tangent of 20 degrees is about 0.36, meaning that it’s equivalent to the worst hills in San Francisco. Let’s take 20 degrees as our upper limit for the ramp angle.
Similarly to how we dealt with distance, we can break down the velocity using the hypotenuse rule.
That means, if Alessandro is driving at 100 miles/hr, or at 44 m/sec, and he’s on a 20-degree ramp, his forward velocity (vh) = 0.94*44 = 41 m/sec. (I’m using the formula that cos theta = 0.94 (I looked that up) = adjacent / hypotenuse, and the adjacent is the forward velocity vh, and the hypotenuse is the total velocity v. So re-arranging that equation, we get vh = ( cos theta)*v = 0.94*v = 0.94* 44 = 41 m/sec.
Similarly, the upward-moving velocity, vu, = (sin theta)*v = 0.34*44 = 15 (approx) m/sec.
So every second that Alessandro’s on the ramp, he moves forward by 41 meters, and up by 15 meters.
After Alessandro leaves the ramp, he will continue moving forward by 41 m/sec, and he’ll also have his own upward velocity. Then he’ll also have the pull of gravity, which increases every second – and will shortly start moving the car down instead of up.
Let’s work through a little scenario.
Suppose that Alessandro flies off the (20-degree) ramp at 100 mi/hr, meaning his upward velocity is 15 meters/sec. In the first second, his upward-moving velocity will take him a total of 15 meters up. (15 meters/sec * 1 sec = 15 meters. Watch the units.)
In the same second, the force of gravity will exert itself on the car. The ACCELERATION due to gravity is -9.8 m/sec-squared. To make our lives easy, let’s call this -10 m/sec-squared. The total distance that gravity will pull Alessandro’s car DOWN is in meters; it is -10 (meters /sec-squared)*(1 sec)(squared) = -10(1 squared) = -10 meters.
It looks like this:
– At zero seconds, zero meters down. (But zero meters up, also.)
– At 1 second, 1-second-squared is still 1, and -10 * 1 = -10. The force of gravity pulls Alessandro’s car down ten meters. However, based on the previous calculations, if he’s going 100 mi/hr (44 m/ sec), on a 20-degree ramp, then his vertical motion up is 15 meters. So combining the upward (+15) and downward (-10) vertical velocities, Alessandro’s car is up 5 meters at the end of one second.
He doesn’t have a lot more time, though.
At the end of two seconds, his vertical position due to gravity is:
position = -10*(sec-squared) = 10*(2*2) = -40.
At the end of two seconds, he moves down 40 meters due to gravity. He moves up only 15(m/sec) * 2 (sec) = 30 meters.
So he’s 30 meters up, and 40 meters down, so he’s 10 meters under the surface of the earth. Meaning squashed like a bug. UNLESS he’s connected gently with the next ramp, and is moving forward.
So Alessandro, under these conditions, easily has one second, but definitely not two, for covering the distance between the two ramps.
So we backtrack and ask ourselves about his forward position at the end of that first second.
His forward position will be his forward velocity * 1 second, = 41 (m/sec) * 1 (sec) = 41 m.
At the end of one second, Alessandro has moved forward by 41 m.
You were saying that there’s a 6m separation between the two ramps.
So, he’s not crashed to the earth in that time.
If you’ve got a 6m separation, then the first six meters of the 41 m that he covers going forward will be over empty space. The remaining 41 – 6 = 35 m will be over that second ramp. And he’s 5 m up from where he left off from ramp 1.
So at the end of the first second, Alessandro and Catalina have covered 41 meters going forward. They’ve gotten over the six meter separation, and have moved forward another 35 meters over the other ramp. They’re also 5 meters in the air ABOVE where they left off the previous ramp.
But that’s five meters up, and the ramp is pointing down. And at that speed, it will be while before they connect with the ramp (or earth) again, and it is really going to HURT.
So I’d play with things for a bit. I might use a less-steep ramp, because they will have moved forward a bit more at the end of one second, but be up a little less.
And yes, you can solve this whole thing analytically, but I feel it might be smarter to just estimate some scenarios and see how they work out, because you want realistic values for things like (relative) ramp heights, ramp angles (thetas), distance between the ramps, velocities, and doing this will give you a value for how fast they’ll be moving downward (velocity down) when they DO connect with the second ramp, because that will certainly be jarring!
The important thing will really be that downward velocity when they connect with ramp 2.
If it were me, I’d put together a few scenarios using Excel, just to plot out heights and vertical velocities for different versions of ramp angles, and maybe different car speeds. Because the important thing is to get the angles so that the car connects more-or-less gently with ramp 2. (As in, vertical velocity going down is close to zero.)
Does this help?
Wishing you the best!
It helps me, if not the Authorlords, cos gravity while in the gap needs to be accounted for.
Thank you!
+1 Lovely statement and easily understood! Thank you.
Thanks, Berry!
You are awesome. And you are right. It did hurt when they landed.
Hi, Ilona –
Woke up thinking about this a bit more.
If you want, I can take the next step … figure out how far out on ramp 2 Alessandro’s car should land, and a desired h (= h1-h2), and a more reasonable value for the velocity, then back-compute to a good ramp angle theta. That would give you all the deets needed to write the set-up – the angles of the incline, the velocity that Alessandro would need to achieve on the ramp before flying off, how much of a “thud” they have when they hit – because even if the back end gently grazes ramp 2, the front end will be “falling” an amount (because where it hits on ramp 2 will be further down from where the back end hits) – and thus the total downward velocity of the front-end; this would let you know whether it’s a gentle “thud” or a tire-busting, head-through-the-roof thing.
So I’d have to be a bit precise about this.
Let me know if this would be helpful! – A.
I can’t believe I’m saying this, but I kinda sorta understood this – thanks!
You’re welcome, Sam!
you should ask this on reddit, that’s were all the nerds are lmao
Lol!!!! ?
I only have one thing to toss in here: Bernoulli effect!
This discussion reminds me of a longstanding, hilarious argument with a friend who didn’t understand why race cars didn’t fly off the track at high speeds. Otherwise a very intelligent person, but this just escaped him. 🙂
I appreciate that you want Catalina’s math to be right. However, I think of Alessandro as a James Bond type. I fully expect the car to either sprout wings or trigger a booster rocket once it’s airborne. Either way, Grandma Frida will want to get her hands on that baby.
Yaaassssss
I worry you’ve made this too complicated. The moment the car leaves the ramp (or loses contact with the ground for any reason) it is in pure projectile motion. It’s like you have thrown a rock.
https://en.wikipedia.org/wiki/Projectile_motion
In projectile motion your velocity (which is a *vector*) is constant – you’re just trading off horizontal velocity for vertical velocity depending on where you are on the curve. (Yes, there is air resistance, but we can ignore air resistance over such a short distance and given a reasonably aerodynamic car). This is the reason why racing cars *never* want to lose contact with the road: in sports like WRC (rally cars) when you take off on a bump you are throwing away horizontal velocity (which is what you need to win a race) for vertical velocity (which gets you nothing).
So I think at the moment you leave the ramp you call that launching a projectile at x_0 = 0, y_0 = 0 , v_0 = the speedometer reading of the car and then you just use the projectile equation for reach (distance) from the Wikipedia page above:
d={\frac {v^{2}\sin(2\theta )}{g}}
You know you want d to be 6 meters or whatever, so the velocity is the square root of g times d divided by sine(2*theta)
Hmmmm wait a minute have to take my shoes off for this one
Nope. You are forgetting the height difference between both sides. Your equation is the special case for height difference zero.
Well the equation is also assuming that the car is a dimensionless projectile, whereas in fact you want to get the back wheels past the gap. Assuming the difference between h1 and h2 is relatively small as pictured, it is a reasonable approximation, since the amount h2 is lower than h1 is essentially all safety margin.
All I’m saying is, if I was headed at high speed in a vehicle at a drawbridge or whatever, that is the equation I’d do – it’s both simpler to do and it’s the most conservative calculation to make.
I should also add that while the diagram shows h2’s edge is lower than h1, you wouldn’t really be able to tell that without prior knowledge of the area – you are barreling up a ramp at high speed, and if I can’t see h2 being *higher* than h1, I would assume the worst case scenario, which is h2==h1.
It’s an action scene, not a thesis defense. You’re trying not to die.
Is that equivalent to
https://en.wikipedia.org/wiki/Range_of_a_projectile
d=6 solve for v?
Assuming no air resistance
and y0 = h
Engineering was 30 years ago… sorry. I got the stainless steel ring and then took accounting.
I think in a high speed chase he wouldn’t know the height difference, so should just assume they are the same. Also air resistance is very hard to calculate and doesn’t take into account wind and other air currents that you would get in a dynamic location such as a canyon, around tall buildings or over water.
Math is hard and I think a simple equation such as above were you take a better safe than sorry attitude + Magic and viola!
Short answer 1: They make it across the gap, but hit the other side, tumble and roll and end in a fiery crash, thereby ending the story and this arc of the series.
Short answer 2: and then MAGIC happens. They successfully make it across the gap, however their pursuers chicken out, hit the brakes too late and end in a fiery heap at the bottom. All is well. As it must be, or the story could not continue!
(Once upon a time, I passed 4 quarters of college calculus & differential equations, plus linear algebra and a slew of other math courses. I failed physics every time I tried. Apparently, I has not the brain for physics.)
Lol sorry Aglaia my car plopped onto my tablet
This is why I didn’t take physics. Biology? Yes. Chemistry? Yes. Physics? No. My head hurts.
Hey, this will be embarrassing if I am wrong as I am a maths teacher but it is almost 10:30pm here and I’ve been up since 4:30am so fingers crossed!
If you want to do it this way you are very close, but I think you forgot to square a 6 when you subbed in t from the horizontal direction and also there might be an incorrect sign (I think this is caused by maybe making some elements negative or positive inconsistently vertically).
So I think you get 9.8x 36 on the top of the fraction and 2(6tan(th) +h)cos^2(th) on the bottom before you square root.
I tried taking a picture of my working out but the file is too large – I’m happy to be contacted by email if it helps (it would be nice to give something back for your amazing stories!).
I’m going to give this problem to my class tomorrow and get them to solve it – maybe they’ll all discover great new authors at the same time!
Whoaa your students are very fortunate to have you as their teacher!
You. Rule.
Oh boy. I don’t math. Pretty much ever, lol. I celebrated in college when I took my last, evil math class. I mean, my father-in-law is a retired math teacher. I could always ask him if you really need me to. But I’d rather avoid what is sure to be an at least 30 minute discussion about math if I can help it. 😀
Ditto. Except replace “math teacher” with physics teacher. Or “father in law” with “partner” and “math teacher” with “chemistry teacher”. Either way, that’s 30 minutes I’d rather spend reading XD
I feel the need.
The need for speed.
+1 ?
My dad was a high school physics teacher, but he was more into having his class build bridges instead of flying cars across a gap.
Well, thank you, ilona andrews, for the stimulating post. Unfortunately I am chauffeuring a sibling today so I am warming a chair in waiting room. I will take look at this tonight when I finally get home. Umm, no, make that tomorrow.
Meanwhile physics and math aside, it is the story magic that counts for me. Dad used to say believe one impossible thing when we would discuss a science fiction story with him. Beside James Bond was 007 and secretly magically enhanced to us girls as Sean Connory was the thing then. Dad would love this question as it would appeal to the engineer in him. Unfortunately he crossed the Rainbow Bridge several years ago. But I am sure the BDH can resolve whatever the issue is.
This is a foreign language to me. Looking at it, my brain starts swirling aimlessly around going : “Wha-wha! Wha-wha! Whaaaaa…”
Me, too! Maths are my kryptonite.
+1 – if it isn’t simple math, then I’m done ??
Funnies are always the best policy.
As to your equation even if the projectile formula gives you a number I have not seen anything as to the actual mass of the vehicle and contents. Without that info I could not say if it would make the gap or not.
But it is great that you want to be realistic, this is why I like your stories so much!
Nope. Mass does not enter into this equation. A feather and a ball made from lead drop at the same speed (in vacuum).
To be EXTRA pedantic the mass does make a difference. The mass of the object also pulls Earth (or whatever is producing the closest gravity field). So an extremely heavy object such as a tiny black hole would indeed reach the ground faster, because the ground would also be coming toward it.
Of course unless the mass is within the same order of magnitude of Earth we can generally just ignore it.
My guys are asking how much the car weighs too.
Ok, with all that +- confusion you are practically asking for nerdy physics jokes. For example this one:
A mathematician, an engineer and a theoretic physicist are given the task of calculating 1 + 1. The mathematician is in deep thoughts for 20 minutes and finally concludes “a number x exists so that x = 1 + 1 is true”.
The engineer pulls out his slide rule and calculates “1 + 1 = 1.99999”.
The theoretic physicist fills several sheets of paper with calculations and gets the result “10 to the power of 1000”.
The other two look at him with big eyes and ask him: “Are you sure?” He answers: „Well, the order of magnitude might be a bit off, but at least the sign is correct.“
That was a great joke! Yes, I am a nerdy quasi physicist!
You forgot the statistician. The statistician would create a hypothesis test to find out the probability that 1+1 does equal 2. I had to do something very similar to that in a mathematical statistics class. Thank goodness I do applied biostatistics. ?
Here, this is a pretty good explanation.
https://physics.stackexchange.com/questions/175381/speed-needed-to-make-a-car-jump-from-a-ramp
Sent to a geek mailing list I belong too… I’ll let you know… (a bunch of physicists and engineers and computer geeks… someone will figure it out. Tho there will be a dozen smart ass answers too).
I keep thinking of a secondary magic of Luck, but only in cases of possible death or injury.
This has been an entertaining read tho.
I was a biology major forced to take physics…. I didn’t do very well lol … it looks great to me. I read, say yes that’s fine, and move on… love you guys for wanting to have it correct!!!
See https://en.wikipedia.org/wiki/Projectile_motion#Displacement
y = -h
x = L = 6m
v0 = sqrt((6*6*9.8)/(6 * sin (2*theta) + 2h cos^2 (theta))
Of course it theta or h is two large the car will end up doing a nose dive into the second ramp, and x should probably be taken as > 6m, to ensure you actually will hit the ramp safety, the math would have you hitting the ramp right on the edge which could potentially result in the car pivoting and falling backwards off the ramp depending on the exact geometry and angles involved.
It’s simple. Tuna on rye with a side of garlic dill pickle.
Sorry. I guess I’m hungry.
Another Wikipedia page that might help is the Range of a Projectile page. The equation for range appears to differ from yours a bit.
Where is Niels Bohr when you need him? ?
https://www.ideaconnection.com/blog/a-story-about-a-physics-exam.html
Ahhhmmmm.
D) All of the above.
What Molly wrote
Air resistance/drag is going to play some role, and one that will vary from car to car. For example, a big boxy truck will need to push a lot more air out of its way than a sports car.
Sorry to make Catalina’s life more difficult with an extra variable.
While I was teaching my Calculus II class I had the physics professor working on this. He and I agree that you have two errors in the formula that Catalina came up with. One is small (the 6m^2 in the numerator should be a 36m^2) and one of them more significant. the minus sign that you have between h and 6 tangent theta should actually be a plus.
Here is how you can tell that the minus sign cannot be correct. If the ramps were the same height, making the differences in the heights be zero, which makes h=0, then the first formula results in a negative number under a square root sign, which is not possible if your answer is a real number. In the corrected version of the formula, having h=0 still results in a real answer.
Hope this helps!
I just keep thinking “How’d Evil Knievel figure it out? He was no math genius.” Probably why he crashed more than once. I’d expect a simplified version of this information would be available in a “stuntman’s handbook” somewhere. Overall weight, speed and angle of ascent will give you rate of forward motion and fall speed. Even mathematical geniuses take shortcuts. E=mc2. So simple yet elegant.
OK. Forget the complex equations, sin(theta), blah blah blah.
The 10-degree upwards vertical component of the trajectory can be thrown out as negligible. That 10 degrees only means something if h1=h2; i.e. the parabolic flight pattern must have its high point midway along the jump. (I am saying this as a certifiable maths person; I have a degree and everything!) Since your equation parameters state that the start is higher than the endpoint, throw out theta.
From a physics standpoint, it still makes sense to disregard the initial upwards velocity because you have to make sure the ENTIRE car makes it across the jump, not just the front. None of the standard equations take into account the physical shape of the object. Is it a front wheel or a rear wheel drive car? All wheel? These factors will also affect the velocity at the time of take off, and the center of mass of the vehicle and all its occupants will affect its momentum as well.
Unnecessary complications aside: if you solve for a purely horizontal takeoff, clearing the height difference would mean making the time it takes for gravity to drop the vehicle h feet equal to the time it takes for the car to travel L horizontally. So t = sqrt(2*h/9.8) and also t=L/v. Setting these equations equal to each other since time is the same, sqrt(2*h/9.8)=L/v.
Solving for v: v=L/[sqrt(2*h/9.8)].
Where are the damn flying cars they promised us, I ask ya?
You left out a key component of the equation. Are they driving a gas- or electric-powered car?
And is anyone else picturing them trying this with a Smart Car? You’d have to add wind as a factor. 😛
Love this post, had a lot of fun reading the comments, but am glad I didn’t major in physics (even as my father – an evil physics engineer and university prof – tried to feed it to me since I was a babe). I know the basics and how to look it up in the books. That’s enough for me.
I wanted to tease my kid3 (a math wizard) with it, so she took a look and chickened out with the comment: (Her grades in physics and chemistry were straight As ;-). Now she works for her points to go and study psychology).
So Alessandro has to do a little magic otherwise Catalina would be right.
OK, somehow the comment from Kid3 didn’t show, so here it is:
Mom that is physics not math! You know I dropped it 2 years ago, but with the looks of the sketch the car crashes!
Makes me wonder how I passed Math classed in high school and college
My son, who is taking Calculus I at college, says that there are too many variables. Need to know a value for h and for theta in order to solve for V.
If you have those values he is more than happy to help……this is all another language to me 🙂
I ended up getting the same formula you show in your picture. Rather than spam more people with my math, I just set time of flight to L/(v*cos(theta)), and height dropped to vt*sin(theta)-4.9 t^2; solve for v.
I hope that helps!
Okay, so very simplified… if we assume that the impact of the angle is negligible and the maximum reasonable velocity of the car is 80m/s (just under 180mph) the hight difference must be greater than 4.5m. Which basically means that jumping gaps is not a great idea, but then we knew that without the math 🙂
In the midst of this dark time in American history all these great useful comments give me hope! We got this! Happy daze.
My head hurts just trying to work this out.
This broke my brain. I Worked as a tech writer for many years, I can write computer programs, but I cannot do math. I broke my brain looking at the pictures and reading the words. Now I’m at the state of Math bad, tree pretty.
OMG! BUFFY FOREVER
I paid for a mathematics degree from Rice University. I just sent it a text with a screenshot.
It did ask if it could be invoiced…
Ugh
Math. No. Just no.
Not sure what you’re looking for, but I can tell you that it reminds me of the Dukes of Hazzard… Just go really fast buckle up and you’ll be okay ?
(Or not) ?
If it’s for a scene in one of your latest books aren’t we being a tad to … Um.. precise? What does your story need?. You guys always make it work.. you’ve thrown science out the window before ??❤️
LOL, I had the Dukes of Hazzard thoughts as well.
What kind of car are you using because that would factor into the equation?
With enough magic all things are possible….
A Smart Car?! Alessandro wouldn’t drive a Smart Car. He drove a Maserati. So, I wonder if he was driving it while flying through the air? I know, I know read the book. ?
This was in response to Tink’s comment,
My husband did math for 9 hours today and then came home and did this math for fun b/c I asked him to. He asks for an extra steamy scene in the book to thank him!
He says the 6m2 should be 36m2
*Pencil drop* #ignoringfriction. He is now ad-libbing this scene and it is hilarious. Don’t try to ramp a car with an engineer on board.
Coming late to this, my thought are, math and physics are good, it is possible, reality is what happens to the rear end and suspension of the car?
Everyone who says that you need to square the (6m)^2 is correct. That is what you find when you do a unit check to get a velocity in m/s. Also your equation does need to take into account what is positive h and what is negative. If you look at the links posted above and take into account proper sign (h=h2-h1) G=-9.8m/s^2. The links posted were:
https://physics.stackexchange.com/questions/175381/speed-needed-to-make-a-car-jump-from-a-ramp
https://en.wikipedia.org/wiki/Projectile_motion#Displacement
And you plug them into wolframalpha correctly as noted here:
https://www.wolframalpha.com/input/?i=%E2%88%9A((9.8*L%5E2)%2F(L*sin(2%CE%B8)-2*h*cos(%CE%B8)%5E2)),L%3D6
https://www.wolframalpha.com/input/?i=%E2%88%9A((-9.8*L%5E2)%2F(2(h-L*tan(%CE%B8))*cos(%CE%B8)%5E2)),L%3D6
You get a consistent answer. You can then play with the h (drop in height is negative number) and angles are in radians (ex, Theta=10deg = .17453rad, h= -1, gives a velocity of 9.4 m/s ) if we make the height difference h=1 so the other ramp is higher and keep the other variables the same, the velocity increases to 56m/s. If you push it too high to say H=20 then you get a nonreal result since its impossible. You can play with the angles and spacing for L and H in this link. I’ve included the conversion for theta from degrees to radians so it makes more sense.
https://www.wolframalpha.com/input/?i=%E2%88%9A((-9.8*L%5E2)%2F(2(h-L*tan(%CE%B8))*cos(%CE%B8)%5E2)),L%3D6,h%3D1,%CE%B8%3D10*%CF%80%2F180
This is my husband. He’s a rocket scientist. Literally.
.
I love your books!
Nice!
Umm, sometimes I just skip things when I am reading to get to the goodie
All I know is math is a four letter word.
Good luck. May the odds be ever in your favor.
It’s been way too long since I’ve thought about this stuff. I believe the equation is pretty much correct except for a couple housekeeping things. As noted by others, the 6 m in the numerator needs to be squared. Either 36 m^2 or (6 m)^2. The second option is “truer” to the kinematic derivation but perhaps the former is easier to read and/or type.
Another thing is whether you’re adding or subtracting in the denominator. I agree with subtraction. Did you specify whether the car is landing at a height above or below where it started and I just missed it? Customarily, we would define h as h-final minus h-initial (and maybe call it “delta h” while we’re at it). If the final height is less than the starting height, then this number is negative. And if we subtract a negative number, it looks like addition…and we could choose to write that shortcut into our formula. It’s also theoretically feasible for the final height to be greater, like the car needs to land during the upward part of its trajectory. Clearly, that’s a scenario fraught with fraughtiness, but in that case delta h is a positive number.
Of course, you’ve stated that h is the initial velocity minus the final, which reverses most of the signs in the previous paragraph. If I could plead for one change, it would be to use final minus initial. But is this also why you have h – 6tan(theta) instead of 6tan(theta) – h? Those two changes do work together, although it makes me twitch to concede that. Or are you secretly treating g as -9.8 m/s^2…?
Several people have pointed out that the car risks plowing into its landing platform. The fix is to replace the equation with an inequality. That is, the velocity must be greater than or equal to the lovely radical on the right hand side.
And the version of the equation that uses sin(2*theta) collapses into the same equation you have, after you bludgeon it with a trig identity.
I propose v >= sqrt(((9.8 m/s^2)(6 m)^2))/(2((6 m)tan(theta) – h)cos^2(theta))),
which is a hot mess without an equation editor! And anything here that looks like a question is rhetorical. ?
Good luck!
My husband, who was sure he could solve this in 10 minutes, stopped at 8 minutes and said to tell you that your driver, at the moment he or she realizes what’s ahead, should close both eyes and stomp on the accelerator.
I’m a librarian who Is now referring you to the post from the rocket scientist for an answer. As a reader, I can definitely say that I can live with “the car flew over the gap” without the brain breaking math.
Is the engine in the front or back of the car? Weight distribution will impact how it lands.
This is an explanation for the math of an Evel Knievel motorcycle jump.
https://youtu.be/FZ0td-SCzPo
A few have already caught the two errors I think are there: in the numerator it should be a 36 (instead of 6) and in the denominator the subtraction needs to be changed to addition. This assumes that the height of the jump-off ramp is higher than that of the landing-ramp and that ‘h’ is the magnitude of that difference in height (and so a positive number). I tried writing up my solution and attaching the picture – hopefully it is readable and understandable.
All of the above models the car as a particle: it has no dimension and is not a deformable body. It also neglects the effects of air drag. Neglecting air drag probably reasonable: will depend on the aerodynamics of the car and likely minor. And I think you can reasonably neglect the deformability of the car (unless the car is very long, I don’t expect any significant bending or twisting of the car to be happening). However, neglecting the dimensions of the car can lead to significant differences in the result, even when treating it as a rigid body. One of the issues is the location of the center of mass of the car – is it close to the geometric center? If not, you’ll see the car rotate about that geometric center – if a car is front-heavy, that is why the front/nose of the car will start to dip relative to the center of the car. This is also all impacted by the wheels – even in mid-flight, as whether they keep spinning or not will impact angular momentum. This now becomes a much more complex problem…
+1 I’m really bad at Maths. Your discription makes logical sense for the bits that ican understand- the diagram though is blowing my mind
I have taught this stuff many times in calculus classes.
It seems that you intend L = 6 m, which you did not mention. If that is so, your formula is almost correct. To fix it, you should change the “minus 6” in the denominator to “+ 6 m”. Then you have a correct formula for the flight of a tiny particle that does not encounter air resistance as it flies exactly from the vertical edge of one wedge to the vertical edge of the other. You might think of applying this to the bottom point on the front wheels. If I were actually going to do fly this gap, in car or motorcycle, I would use the formula, then increase the speed by fifty percent, or maybe even double it, to be safe. Then I would try it with a crash dummy before I tried it with my own body.
Hmmm… I have L=6 defined near the top as one of the givens… I don’t see the negative you mention in the denominator (though it was on the original posted solution, so maybe your reply was to the original post and not to mine?) . It does almost look like there is a negative in the numerator… That is a scanner problem.
And I teach this topic to entering students on a regular basis at the University level. Dynamics is my area of specialization both in teaching as well as research. So this was a fun little review problem for me. 🙂
You need to factor in the weight of the car plus the weight of what/who it is carrying.
Most cars are aerodynamic shaped – decreased air resistance.
NASA has a branch in Texas, their computers could spit out the equation in a blink?
The answer is 42. ?
Yes!!!! “Eddie’s in the space time continuum” will account for anything. (Oh I needed that this morning!!) (Eddie who?)
LOL! GO DOUGLAS ADAMS! How wheres my towel?
If we are ignoring wind resistance, centripetal rotation, and the rest of that stuff, and treating this like a simplified physics question then the easiest solution would be as follows:
Let @ represent the angle of the incline, H be the height difference from the end of the incline to the edge of the “landing point”, L be the horizontal distance between the incline and the “landing point”, and V be the speed of the vehicle on the incline, thus Vx is the horizontal speed of the vehicle. By the properties of triangles, Vx = V*cos@. Since the vehicle must travel the distance L within a given amount of time T, based on Vx, we can say Vx*T=L, thus T=L/Vx or T=L/(V*cos@).
Given this, we also know that the vehicle must land at the “landing point” after T seconds, and not below it. Therefore, let Vy be the vertical velocity of the vehicle. By the simple equation for distance (D), we know that D=Dstart + V*T+A*(T^2)/2, where A is the acceleration. In this case, A is gravity with a value of 9.8meters/(second^2), D is H, and Dstart is 0 (zero, though it makes little difference if D is 0 and Dstart is H, or if D is H2 and Dstart is H1, as given in the question), and V is actually Vy, or V*sin@ (by the properties of triangles).
Hence, H=Vy*T-9.8*(T^2)/2, equivalent to H=Vy*T-4.9*(T^2), for simplicity. Substituting V*sin@ for Vy and L/(V*cos@) for T, we get H=V*sin@*L/(V*cos@)-4.9*(L^2)/((V*cos@)^2). Simplifying, this becomes H=L*tan@-4.9*(L^2)/((V^2)*((cos@)^2).
By moving the V components to one side and the rest of the components to the other side gives: 4.9*(L^2)/((V^2)*((cos@)^2))=L*tan@-H. Solving to get V by itself on one side of the equality gives us this result:
V^2 = numerator [4.9*(L^2)] / denominator [L*(sin@)*(cos@) – H*((cos@)^2)]
or: V=sqrt( (9.8*(L^2)) / (2*(L*tan@ – H)*((cos@)^2)) (your answer, * -1)
So in summary, if L=sqrt(6) or your equation is saying “9.8m/s2 * (6m)^2” in the numerator, then our answers of effectively equal, accounting for a factor of -1 in the denominator, most likely due to variable placements in the vertical distance calculation. I’ll also note, it doesn’t matter if the “landing point” is also a slope, or whether it is above or below the end of the initial incline, so long as you are ignoring the centripetal rotation of the vehicle.
I would be more than happy to assist with this further if you would like to discuss it.
All the best.
All correct, but your definition of H is inverted from the one that Ilona has given, so H = -h.
Precisely the answer I got.
Me, too… what HE said.
I think we neglected momentum …maybe…um…
Gah! It’s already in there. Sorry.
Since h is a drop, the denominator will include the term an addition rather than a subtraction. Also, the numerator will have a 36 rather than a 6 – but you can easily take that out of the square root, to make it 6m * sqrt ( 9.8m/s^2 / [2cos@^2(6tan@ m + h m)] )
My main concern is that the units aren’t carried through in the text. if you start with 36m^2, you should carry on putting the units in for every instance that a length is included.
Heh. That was fun. More! 😀
Yes.
From my genius family member:
I’m unsure what the correct answer is, but that equation would leave you with velocity measured in meters^(1/2) per second, so it can’t be correct.
I’m imagining the car to be an Alfa 4C Spider in red (or maybe black). I have no idea if that’s correct, but that’s the way the “movie” of the jump is playing in my head. Don’t know if the math works, but the jump looks cool! ?
I think it is. We wanted something fast and Italian.
Yay! I imagined correctly even if I couldn’t math correctly! ?
Short answer: It’s easier to think of the cos as being outside the square root, even if it’s not mathematically simplified.
1 (4.9 * L * L)
v= __________ * sqrt { _________________ }
cos(theta) (h + L * tan (theta) )
I don’t know if this would help, but it’d be easier to reverse the question. How fast is it reasonable for the car to be going at the end of a ramp? How high and far of a jump are you looking at? Then calculate your angle. Or how high is the jump and what kind of angle are you looking at? Then calculate your distance. Since you’re making up the scenario, you can decide what numbers you want and then write the scene with information going backwards.
But then again, I don’t know if you’re looking for the correct FORMULA to write into the book and not just the numbers…
However, there are a couple of assumptions being made with this formula. First that the car ceases all upward movement once it leaves the ramp, and second that the car is a point object (as described by at least one other commentator). The answer above was made using the basic equations of motions.
If you’re looking to see if the car has any upward movement after it leaves the ramp, that’s a whole different can of worms. You would need a couple different sets of equations – the first to find out when upward velocity hits zero, and the second for when gravity takes affect. This would be extremely time consuming given the limited information. Again, it would be a lot easier to go about it backwards from what you’re looking for right now.
Can’t wait to read it and find out how you tackle this. 🙂
Arg! The formula looked so good in the comment section!
It should be 1 / cos (theta)
and the square root of
(4.9 * L * L)
/
(h + L * tan (theta) )
Yeah I was considering that the issues are
-how much time will it take the car to travel the horizontal distance btw ramps?
-how much will the car rise after it leaves the first ramp?
-how much will the car drop before it gets to the 2nd ramp?
And in the real world you would need to answer those questions for the back tires of the car, assuming that the front end of the car does not rotate to be lower than the rear axles. This sounds like a problem for a Stunt Coordinator! Know anybody in Hollywood?
I’m pretty sure my head just exploded.
Mine too, but the car landed safely just before the math did me in, LOL.
Mine too, I’m glad that I’m not the only mathematical dunce in the BDH!
Wow! Cudos for all who tried! Including Ilona and Gordon!
My contribution, aside from admiration, is worthless since I definitely don’t know, but I feel your pain… and will happily wait for it to be solved by someone else 🙂
+1 ??
Your fan base is so smart!! Wow!
ditto!
The Mythbusters did this with a bus…
https://www.youtube.com/watch?v=QQE8fYWZMYQ
It worked for Sandy and Keanu with a bus… kinda?
This reminds me of grade five. word problems. I hated grade five word problems. I’m a grown up. I don’t have to do them anymore. If it’s OK to ignore biology by having 5000 year old evil geniuses, it’s OK to abuse physics?
My thoughts exactly
Wrong series! Physics abuse happens in the Innkeeper series!
Practical engineer here. Let’s go build something and test it out!
Hahaha! Fun!
The answer is a flying car from Harry Potter. No math needed then.
LOL! That’s a good one. Here’s another. Alessandro car is tricked out and custom built, with extra weight where it needs to be to ensure its well balance. The entire structure and suspension system is top quality. This is something the AL’s have already made clear in the series with the comments on how a lot of the vehicles used by the Houses are, despite their seeming normal off the lot looks, are custom made with armor with all of the support structure and suspension required. Rogan’s SUV is a very good example. Alessandro knows he and his car can make the jump because he’s done it before. Either because he is asecret James Bond fan and a daredevil at heart, or because the house insisted on special training which happened to include this… Now how well the car fares on the other side …. Yes, all of this additional weight and everything will affect the numbers but remember, the motor will also have to beefed up to compensate for the extra eight. Even if
We all see jumps like this in the movies that we know, or should know is not really possible in real life with out some EXTRA help. Dukes of Hazzard come to mind has well has a couple of cops shows. But we all are willing to suspend disbelieve for the sake of the story and the action.
Has a final, a kudo to the AL’s for wanting to make sure their formula is correct.
AL QUOTE:
Update: everything is funnies to you, isn’t it?
Life is too short to stress out over the big things, that’s way I always eat desert first. 😛
Or Chitty-Chitty Bang-Bang.
Only just read this and as I gave up Physics and Maths after my O levels, I channeled my inner Tom Petty and started singing – I got as far as Learning to fly but I ain’t got wings when my 5 year old grandson asked how could I fly without wings then answered his own question with: Jetpacks!
Forget the equations go for jetpacks 😀
All I can say is why would you want to?
Hmm the physics break my brain! The only reason I even passed physics at o levels was (1) teacher and (2) being an asian, fail is a 4 letter bad word.
I meant to emphasis cute teacher
Dang it , Jim, I’m a chemist, not a physicist.
And this type of thing is why !!!! 😉
Can’t wait to read how it comes out !
My husband LOVES math and physics… I’ve sent this post his way… we’ll see if he has an answer different than those above. 😉
To all those above, including Ilona and Gordon… congratulations for making my head explode 20 minutes into work. 😉 You guys are awesome… I hate math. xD
owwwwwwwww, my brain hurrrrttts
It’s your universe. Forget the maths and provide Alessandro with a secondary, here-to-fore unknown, talent.
I can totally get behind this!
Well, they have said that lots of primes have secret secondary talents, so this wouldn’t be too far fetched. Kind of a cop out though and the AL don’t usually go for those.
Legend says that When the Star Trek pilot screenplay was reviewed there were a multitude of pages which gave a precise description for a shuttle to get from the Enterprise to the surface of the planet. Filming this scene would have taken up over half the pilot to show. Roddenberry put a pen through the scene and just wrote “the crew transported down to the planet surface”?
Awesome story / urban legend!
The math – it hurts. It HURTS!
As someone who used to watch “The Dukes of Hazzard”, the car makes it across just fine.
Nice!
I can’t help with the math, but….. Mythbusters did try to recreate the Dukes of Hazard car jump in one of their episodes. Special episode 9 – Mega Movie Myths. Wikipedia said the episode came out in 2006. Hopefully that might help with some of the practicalities of what you’re trying to do.
https://www.discovery.com/tv-shows/mythbusters/videos/jumpin-a-gorge
nice very good news ,thanks
The equation is wrong. Here’s how to think about it. (Simplifying assumptions are at the end.)
1) The car’s speed on the ramp is V. Therefore its vertical velocity Vv is Vsin@, and its horizontal velocity Vh is Vcos@.
2) The hang time t is just the horizontal gap L over the horizontal velocity Vh. Here L = 6m (abt 20 feet).
3) The vertical distance travelled by the car in the air is t*Vv + 4.9*t^2. (Because 9.8 m/s/s is the acceleration of gravity.)
4) So for example, assuming:
a 6 degree angle (which corresponds to a 10.4% grade, or about as steep as you’d ever see on a paved road);
speed of 22 m/s (abt 50 mph);
horizontal gap of 6m (abt 20 feet); then
the vertical rise across the gap is .27m.
For a 12 degree angle (like a severe jeep track) and 30 mph, the rise is about .25m.
For a 6 degree angle at 100 mph, the car can span 137 feet before it comes down to its takeoff height.
Hope this helps – Excel on request.
Rob
This would be rather terrifying as, most cars do not have a center of mass in the center of the car. To either have the car tip forward (watching the ground come rushing at you) if the engine is in the front, or to not see the ground at all (if it is in the back). Also is the car front or rear wheel drive? That changes the effective gap by the length of the car.
So in future these jumps need to be made in very-well-balanced electric cars. Just don’t split the battery open.
Hi Ilona,
I am a fan who also happens to be a high school physics teacher. I teach regular and AP Physics. As I was reading your blog last night, I really wanted to help. Part of the problem is what you are wanting to accomplish physics-wise in your scene. I found this short tutorial on youtube:
https://www.youtube.com/watch?v=rNvaEnZT0u4
It is only about four minutes long but is exactly about a ramp jumping to another ramp. I think this will help you isolate what you really want to know. Just plug in your numbers 🙂
Hopefully this helps.
To be completely honest, I totally skimmed/skipped this part.
I trust you 100% .
I found other results in the posts that match mine but with numbers. I left everything with letter si it is as understandable as possible. Hope it helps.
I will willingly suspend all disbelief on the car making the jump as long as you don’t throw anymore Thetas at us…. promise ?
I expect this is too late to be of use, but I asked my cousin and he was able to answer right off the top of his head as follows (the blighter!):
It is almost correct. The quick way to see that it isn’t correct is that if you put in h=0 (both are at the same height), the equation turns out to be the square root of a negative number – which isn’t very useful. But someone just made a mistake with the minus sign – it should be plus not minus.
The correct equation is the same except that the bottom line of the fraction should be 2(h + Ltanθ)cos2(superscript not working for some reason?)θ. And there is a typo in the top line of the fraction as it should be gL2(superscript) or 9.8*62(superscript).
Incidentally, to be completely accurate, this is far more a physics questions than a maths question.
I don’t do math but I am wondering if you were quoting Squealy Dan from Letterkenny there at the end ?
Don’t the fancy supercars have aerodynamic shaping to pull the body close to the ground at high speeds so that the wheels get good traction?
Which means that aerodynamics cannot be ignored and your car cannot be modeled as a point mass.
That being said, if the car in flight could be adjusted to act as a wing, it would ‘fly’ much further than a point mass. But also if the front pulls down in flight (due to engine or aerodynamic stablisation), the front wheels would descend much sooner than a point mass only affected by gravity.
My brain is so simple that I just assumed all the pretty numbers were right. Flying car. Wheeeee. Feel free to leave it as is ;). I’m also assuming you aren’t going to pancake Lina…
Nope. She’s gone in chapter 4. Arabella takes over.
Of course, they’re not pancaking Catalina!
I don’t think ….